원 채우기

기하학에서 원 채우기는 (크기가 동일하거나 다양한) 주어진 표면에서 겁침이 일어나지 않고 모든 원이 서로 접촉하도록 하는 원의 배열에 관한 연구이다. 배열의 관련 채우기 밀도 η는 표면에서 원이 차지하고 있는 비율이다. 높은 차원으로 일반화도 가능하다 - 이것 중 동일한 구만 다루는 문제는 구 채우기라고 부른다.
원은 유클리드 평면에서 0.9069의 상대적으로 낮은 최대 채우기 밀도를 가지지만, 가능한 최소 밀도는 아니다. 평면에서 "최악"의 채우기 모양은 알려지지 않았지만, 매끄러운 팔각형은 채우기 밀도가 0.902414로 원점대칭인 볼록한 도형 중에서 채우기 밀도가 가장 낮다.[1] 다각형 별과 같은 오목한 다각형의 채우기 밀도는 임의적으로 작을 수 있다.
일반적으로 원 채우기라고 알려진 수학 분야는 임의의 크기의 원의 채우기의 기하학과 조합과 관련이 있다: 이 때문에 등각 사상, 리만 곡면 등의 이산 해석을 준다.
평면에 채우기[편집]


2차원 유클리드 공간에서, 조제프루이 라그랑주는 1773년에 원의 가장 조밀한 배열 격자는 육각형 채우기 배열이라는 것을 증명했다. 육각형 채우기 배열은 원의 중심이 육각형 격자(벌집과 같이 열이 늘어져 있다)에 놓여 있고, 각 원은 6개의 원에 둘러 싸여 있다. 배열의 밀도는
1890년에 악셀 투에는 원의 크기가 균일할 때와 균일하지 않을 때에 모든 가능한 채우기 중에서 육각 격자가 가장 밀도가 높다는 것을 보임으로 이것이 최적이라는 것을 처음으로 증명하였다.하지만 그의 증명은 불완정하다. 엄밀한 증명은 1940년에 라즐로 피에스 토스(László Fejes Tóth)가 처음으로 제시하였다.[2]
다른 극단에서 Böröczky는 엄격하게 채워진 원의 임의의 낮은 밀도 배열이 존재함을 증명하였다.[3][4]
균등 채우기[편집]
11개의 평면에서의 균등 타일링을 기반으로 한 11개의 원 채우기가 있다.[5] I이 채우기에서 모든 원은 대칭과 회전으로 다른 모든 원들과 매핑된다. 육각형의 틈은 원 하나로 채워지고 십이각형 틈은 3-균등 채우기를 만들면서 7개의 원으로 채워진다. 두 종류의 틈을 가진 잘린 삼육각형 타일링은 4-균등 채우기로 채울 수 있다. 다듬은 육각형 타일링은 거울상 두 개 가지고 있다.
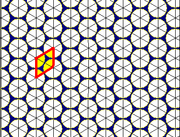 |
 |
 |

|
 |
 |
 |

|
 |
 |
 다듬은 삼육각형 (거울상) |
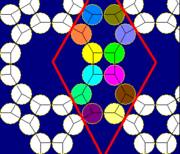 |
구에서 채우기[편집]
관련 문제는 주어진 표면 위에서 움직이고 동일하게 간섭하는 점들치 최소 에너지를 갖게 하는 배열을 결정하는 것이다. 톰슨 문제는 구 표면에서 동일한 전하들의 가장 에너지가 작은 분포를 다룬다. 타메스 문제는 이것의 일반화로 구에서 원의 최소거리를 최대화하는 문제를 다룬다. 이것은 구에서 점전하가 아닌 것을 배열과 유사하다.
제한된 영역에서 채우기[편집]

간단한 경계를 가진 도형 안에서 원 채우기는 유희 수학의 일반적인 종류의 문제이다. 용기의 벽의 영양은 중요하고 육각형 채우기는 원이 적을 때는 최적이 아니다.
동일하지 않은 원[편집]

또한 원의 크기가 동일하지 않은 문제도 존재한다. O이러한 확장은 특정한 두 원의 크기의 시스템(이진 시스템)의 최대 밀도를 찾는 것이다. O오직 9가지의 반지름 비율이 콤팩트 채우기를 가능하게 한다. 콤팩트 채우기는 모든 원의 쌍이 다른 두 원과 접촉하는 채우기이다(접촉한 원의 중심을 이은 선분을 그리면 표면이 삼각형으로 가득차게 된다).[7] 이 반지름 비가 7일 때 콤팩트 채우기는 (위에서 균일한 크기의 원에 나온)최대 채우기 밀도에 도달하는 채우기가 알려져 있다. 가장 높은 채우기 밀도는 0.911627478 이고, 이 때의 반지름 비는 0.545151042이다·[8]
반지름 비가 0.742이상일 때, 이진 혼합물은 균일한 크기의 원의 채우기보다 좋게 채울 수 없다는 것은 알려져 있다. 이보다 작은 밀도의 이진 채우기의 밀도의 상한도 역시 얻어졌다.[9]
원 채우기의 적용[편집]
직교 진폭 변조는 위상-진폭 공간의 원에 원 채우기에 기반한다. 모뎀은 데이터를 2차원 위상-진폭 공간에서 일련의 점으로 전송한다. 두 점 사이의 거리는 전송기의 노이즈의 허용치를 결정하지만 외접하는 원의 지름은 전송기 전력 요구량을 결정한다. 코드 점의 배치가 효율적인 원 채우기의 중심에 있을 때 효율이 최대화 된다. 실제로 디코딩을 단순화 하기 위해서 차선인 직사각형 채우기가 사용된다.
원 채우기는 종이접기 디자인에서도 중요하다. 종이접기의 각 부분은 종이의 원이 필요하다.[10] 로버트 J. 랭은 원 채우기의 수학을 사용해서 복잡한 종이접기 디자인을 돕기 위한 컴퓨터 프로그램을 만들었다.
같이 보기[편집]
참고 문헌[편집]
- Wells D (1991). 《The Penguin Dictionary of Curious and Interesting Geometry》. New York: Penguin Books. 30–31, 167쪽. ISBN 0-14-011813-6.
- Stephenson, Kenneth (December 2003). “Circle Packing: A Mathematical Tale” (PDF). 《Notices of the American Mathematical Society》 50 (11).
각주[편집]
- ↑ Weisstein, Eric Wolfgang. “Smoothed Octagon”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- ↑ Chang, Hai-Chau; Wang, Lih-Chung (2010). “A Simple Proof of Thue's Theorem on Circle Packing”. arXiv:1009.4322 [math.MG].
- ↑ Böröczky, K. (1964). “Über stabile Kreis- und Kugelsysteme”. 《Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae, Sectio Mathematica》 7: 79–82.
- ↑ Kahle, Matthew (2012). “Sparse locally-jammed disk packings”. 《Annals of Combinatorics》 16 (4): 773–780. doi:10.1007/s00026-012-0159-0.
- ↑ 틀:The Geometrical Foundation of Natural Structure (book)
- ↑ Heppes, Aladár (2003년 8월 1일). “Some Densest Two-Size Disc Packings in the Plane”. 《Discrete and Computational Geometry》 30 (2): 241–262. doi:10.1007/s00454-003-0007-6.
- ↑ Tom Kennedy (2006). “Compact packings of the plane with two sizes of discs”. 《Discrete and Computational Geometry》 35 (2): 255–267. arXiv:math/0407145v2. doi:10.1007/s00454-005-1172-4.
- ↑ Kennedy, Tom (2004년 12월 21일). “A densest compact planar packing with two sizes of discs”. 2013년 12월 11일에 확인함.
- ↑ de Laat, David; de Oliveira Filho, Fernando Mario; Vallentin, Frank (2012년 6월 12일). “Upper bounds for packings of spheres of several radii”. 《Forum of Mathematics, Sigma》 2. arXiv:1206.2608. doi:10.1017/fms.2014.24.
- ↑ TED.com lecture on modern origami "Robert Lang on TED Archived 2011년 10월 15일 - 웨이백 머신."

